熱線:021-66110810,66110819
手機:13564362870


熱線:021-66110810,66110819
手機:13564362870
基于應用于圖9和圖10中測量的空間O2和H2O剖面的公式4的通量平衡模型,可以估算燃料電池陰極表面/環境界面處的有效氧和水擴散系數(Deff和DH2O^texteff)。擬合這些空間剖面的初始斜率(從z=0到z=1 mm),該區域最可能符合平面擴散近似,得出DO2^texteff估計值為0.14-0.26 cm2/s,DH2O^texteff估計值為0.21-0.38 cm2/s。這些估計值代表了包含對流(如果有的話)效應的有效擴散系數,對流會增強質量傳輸。
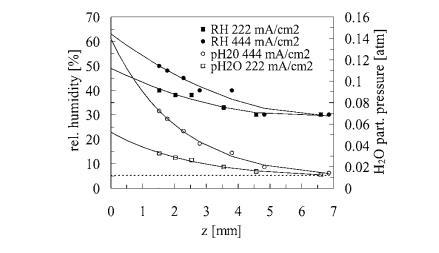
DO2^texteff和DH2O^texteff值與公布的氧氣在空氣中的自由擴散系數D02(對于298 K<T<330 K,為0.24-0.29 cm2/s)以及水蒸氣在空氣中的自由擴散系數DH2O(對于298 K<T<330 K,為0.26-0.30 cm2/s)處于同一數量級。測量的擴散系數與公布值之間的差異可能是由于自然對流的影響、陰極流道中的非平面擴散、以及由于濕度探針的有限體積、實際布拉格光柵溫度與熱電偶讀數之間的差異等引起的RH測量不確定度造成的。作為上述簡單擴散分析的替代方法,我們在此提供傳質系數的估計值。為此,我們使用以下通量平衡方程描述對流傳質:
這里barhm,i是物種i的平均對流傳質系數(cm/s),ci,z=0是z=0處物種i的濃度,而ci,z=infty是物種i的環境濃度。氧氣和水蒸氣的傳質系數估計值以及我們先前建模獲得的值總結在表I中。
| 物種 | 電流密度 [mA/cm 2 ] | 估計值 | 模型值(參考文獻19) |
| hm [cm/s] | hm [cm/s] | ||
| O2 | 222 | 0.47 | 0.56 |
| O2 | 444 | 0.57 | 0.65 |
| H2O | 222 | 0.59 | 0.66 |
| H2O | 444 | 0.69 | 0.77 |
表1本研究中獲得的平均水蒸氣與氧氣對流傳質系數與采用質量與傳熱聯合模型(參見文獻19)在電流密度為222和444 mA/cm2時所得數值的比較。
氧氣的傳質估計值與我們在類似負載和環境條件(20^circC和45%RH)下的近期建模結果一致。在444~mA/cm^2的較高電流密度下,估計的水蒸氣傳質系數與模型預測不同。我們將此歸因于水蒸氣濃度估計的測量不確定度,因為陰極表面的水蒸氣濃度是從陰極肋上方測量的溫度和相對濕度值外推得出的。
與質量通量不同,來自陰極表面的熱通量必須被視為對流和輻射分量的總和,如下列熱通量方程所示:

這里hT是總傳熱系數,可以表示為對流傳熱系數hTc和輻射傳熱系數hTr之和。輻射傳熱系數定義為:
其中varepsilon是表面發射率,sigma是玻爾茲曼常數,Tz=0是z=0處的溫度,Tz=infty是環境溫度。
| 估計值 | 模型值 | ||
| 傳熱 | 電流密度 [mA/cm2] | h [W/m2K] | h ˉ [W/m2K] |
| 輻射 | 222 | 5.9 | 5.6 |
| 輻射 | 444 | 6.3 | 6.0 |
| 對流 | 222 | 11.7 | 10.6 |
| 對流 | 444 | 12.3 | 11.2 |
表II將從圖9所示溫度剖面獲得的平均對流和輻射傳熱系數的估計值與我們先前的建模獲得的值進行了比較。我們假設陰極表面是灰體,發射率為0.9并且是等溫的。用于計算產生熱量的燃料電池電壓在電流負載為222~mA/cm^2時為0.75 V,在電流負載為444~mA/cm^2時為0.63~V。燃料電池陰極產生的熱量不僅取決于燃料電池電壓和電流,還取決于冷凝的產品水比例,這部分水將冷凝潛熱加入到熱通量平衡中。基于我們先前的實驗研究,我們假設在我們的實驗中約有30%的產品水冷凝。估計值與我們的建模預測值吻合良好,差異約為10%。
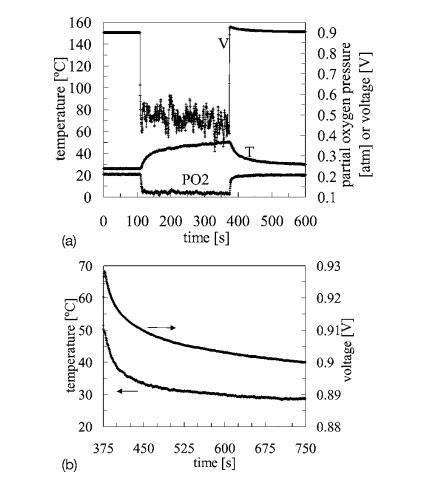
瞬態測量—圖11a顯示了在0和333~mA/cm^2之間的電流中斷脈沖循環期間記錄的電壓、溫度和PO2瞬態。在大約375~s時發生的電壓瞬變在圖11a的尺度上難以分辨,因此在圖11b中提供了放大版本。圖11b中的氧氣瞬變可以擬合到一個單指數模型,時間常數tauO2sim 6~s。這個短的、單一的時間常數可能與邊界層中的O2擴散有關。相比之下,溫度瞬變需要用指數項和線性項進行擬合。指數項(tauTsim 20~s)可能與燃料電池本體的熱質量以及熱邊界層的建立有關。線性項(sim 0.19^circC/min)是由陰極持續積水導致氣體擴散層傳質損失增加,進而引起電池自加熱增加引起的。如果液態水從陰極表面連續去除,則不存在該線性項。
給定測量的氧氣濃度隨時間恢復的數據,可以使用瞬態擴散標度關系估算燃料電池陰極擴散層內的有效氧擴散率。首先,擴散瞬變遵循眾所周知的標度關系:
其中x是與瞬態擴散過程相關的特征長度尺度,D^texteff是有效擴散系數,t是時間。使用從我們的z剖面分析獲得的擴散層估計值(x=deltaO2=0.6~cm),我們可以從公式8中提取有效氧擴散系數的粗略估計。該分析得出DO2^texteffsim 0.06~cm^2/s。這個估計值與先前通量平衡分析[將公式4應用于圖9中的空間O2剖面]獲得的值相似,但略小。我們得出結論,瞬態技術可能由于固有的傳感器響應限制(參見測量程序部分)而略微低估了真實的O2擴散率。測量的O2瞬態弛豫時間(tO2sim 6~s)與固有的O2傳感器速度(tO2text傳感器sim 1.3~s)相當,導致O2瞬態信號的"儀器展寬"。使用更小毛細管直徑的O2微傳感器將提高傳感器速度,但代價是噪聲增加和傳感器穩定性降低。
圖12顯示了在相同的電流負載循環條件(在0和333 mA/cm2之間)下測量的RH和PH2O瞬態。雖然RH信號顯示非常小的瞬態響應,但PH2O響應在恒定電流負載下顯示出較大的變化。PH2O瞬變的初始部分可以用指數函數近似,得出時間常數TH2O~14 s。這個時間常數基本上反映了濕度傳感器的上升時間,因此初始PH2O瞬變時間尺度的精確測量未能實現,但我們可以將其值限定在小于約14 s。隨后PH2O隨時間增加的速度要慢得多,并且是非指數性質的。這種響應表明陰極表面有液態水積聚,如先前所述。當電流在t~1500 s中斷時,PH2O迅速恢復到環境條件,同樣具有約14 s的弛豫時間。(然而這次請注意,PH2O信號沒有表現出次要的線性分量。)另一方面,RH響應顯示出有趣的超調行為。最可能的是,這種超調與濕度傳感器固有響應時間的限制有關(參見濕度傳感器校準部分)。為完整起見,我們注意到,這種超調也可能是由于水生產立即中斷與電池溫度緩慢下降之間的時間滯后造成的。由于這種滯后,陰極上方仍然溫暖的空氣將經歷RH的突然下降,隨著電池(和周圍空氣)冷卻下來,RH presumably會恢復。
結論
本文提供的數據代表了對平面自呼吸電池陰極上方溫度和反應物物種分布的原位測量。這些測量為了解自呼吸燃料電池中熱量和質量傳輸的特性提供了見解。
在IV極化期間,自呼吸燃料電池陰極表面上方的溫度、PO2和PH2O的微傳感器測量反映了這些量隨電流密度增加而發生的顯著變化。觀察到PO2線性下降和PH2O線性增加,這與通量平衡一致。在最大功率點附近RH出現最大值,這與PH2O線性增加和溫度隨電流密度增加呈指數增長相一致。
我們的空間分辨z剖面測量表明,熱和反應物種效應延伸至陰極表面上方達6毫米。互補的y剖面測量顯示,陰極肋結構也明顯影響氧氣分布(盡管肋沿y方向對溫度剖面影響很小)。最重要的是,這些數據表明,熱和物種濃度效應并不局限于GDL,而是延伸到燃料電池陰極表面上方很遠。因為這些效應延伸到陰極表面上方的自由空氣區域很遠,一個主要的啟示是它們會受到燃料電池周圍對流環境變化的顯著影響。這意味著旨在增強自然對流或提供少量強制流動(例如,通過低功率、低速度風扇)的結構修改可能會產生顯著益處。
空間測量用于提供陰極表面上方的擴散和/或對流傳質系數的估計值。這些估計值與氧氣和水在空氣中的自由擴散系數預測值在一個數量級內,相差約兩倍。對流傳質系數也與我們的自由對流質量和熱傳輸模型吻合良好。瞬態測量揭示了與氧氣、水和熱傳輸相關的時間常數存在顯著差異。陰極表面上方的PO2對運行條件的變化反應迅速,具有約6秒的單指數時間常數。相比之下,溫度響應表現出一個指數瞬變,時間常數約20秒,隨后是隨時間線性增加。指數瞬變可能與電池的熱質量以及熱擴散層的建立有關。溫度上升的線性分量很可能與陰極積水和隨后由于傳質損失增加導致的電池自加熱增加有關。在電流加載期間記錄的PH2O瞬變顯示出一個快速的初始指數瞬變;但不幸的是,由于~14秒的固有傳感器響應時間的限制,該PH2O的時間常數未能解析。我們還得出結論,傳感器的瞬態響應速度不足以提供傳質系數的準確估計。
PO2瞬變和熱瞬變的時間常數之間的顯著差異可能可用于解耦質量和熱傳輸效應。我們假設可以采用"氧氣中斷"實驗來進行這種努力。與電流中斷實驗中使用的電流脈沖類似,氧氣中斷實驗將向燃料電池陰極表面輸送強制空氣、氧氣或氬氣的尖銳脈沖,以突然改變氧氣濃度。然后可以記錄和分析燃料電池電流(在恒電位模式下)或電壓(在恒電流模式下)的resulting瞬態響應。盡管對流"脈沖"也可能改變擴散層中的傳熱特性,從而改變陰極溫度,但由于它們不同的時間尺度,質量和熱效應可以彼此解耦。這種解耦也得益于脈沖的傳質影響(例如,對于純氧脈沖,從PO2=0.21 atm到PO2=1 atm,或對于氬氣脈沖,到P02=0 atm)將遠大于脈沖的熱影響(因為增加的對流可能僅導致輕微的溫度變化)。如有機會,我們計劃作為未來工作詳細研究這種用于被動自呼吸燃料電池的氧氣中斷診斷方法。
最后,我們還在進行被動自呼吸燃料電池的建模工作。這些模型利用從本研究中獲得的定量傳輸數據和空間剖面測量,為自呼吸燃料電池陰極中的傳輸提供一個合理的、基于經驗的圖像。這些模型將受益于本文提供的驗證數據,并可能為平面自呼吸燃料電池指明可能的設計改進方向。
 相關新聞
相關新聞
<strike id="yiuck"></strike>
<strike id="yiuck"></strike>